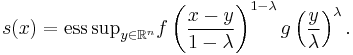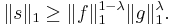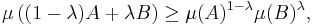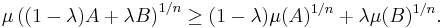Prékopa–Leindler inequality
In mathematics, the Prékopa–Leindler inequality is an integral inequality closely related to the reverse Young's inequality, the Brunn–Minkowski inequality and a number of other important and classical inequalities in analysis. The result is named after the Hungarian mathematicians András Prékopa and László Leindler.
Contents |
Statement of the inequality
Let 0 < λ < 1 and let f, g, h : Rn → [0, +∞) be non-negative real-valued measurable functions defined on n-dimensional Euclidean space Rn. Suppose that these functions satisfy
for all x and y in Rn. Then
Essential form of the inequality
Recall that the essential supremum of a measurable function f : Rn → R is defined by
This notation allows the following essential form of the Prékopa–Leindler inequality: let 0 < λ < 1 and let f, g ∈ L1(Rn; [0, +∞)) be non-negative absolutely integrable functions. Let
Then s is measurable and
The essential supremum form was given in.[1] Its use can change the left side of the inequality. For example, a function g that takes the value 1 at exactly one point will not usually yield a zero left side in the "non-essential sup" form but it will always yield a zero left side in the "essential sup" form.
Relationship to the Brunn–Minkowski inequality
It can be shown that the usual Prékopa–Leindler inequality implies the Brunn–Minkowski inequality in the following form: if 0 < λ < 1 and A and B are bounded, measurable subsets of Rn such that the Minkowski sum (1 − λ)A + λB is also measurable, then
where μ denotes n-dimensional Lebesgue measure. Hence, the Prékopa–Leindler inequality can also be used to prove the Brunn–Minkowski inequality in its more familiar form: if 0 < λ < 1 and A and B are non-empty, bounded, measurable subsets of Rn such that (1 − λ)A + λB is also measurable, then
Notes
- ^ Herm Jan Brascamp and Elliott H. Lieb (1976). "On extensions of the Brunn–Minkowski and Prekopa–Leindler theorems, including inequalities for log concave functions and with an application to the diffusion equation". Journal of Functional Analysis 22 (4): 366–389. doi:10.1016/0022-1236(76)90004-5.
References
- Gardner, Richard J. (2002). "The Brunn–Minkowski inequality". Bull. Amer. Math. Soc. (N.S.) 39 (3): pp. 355–405 (electronic). doi:10.1090/S0273-0979-02-00941-2. ISSN 0273-0979. http://www.ams.org/bull/2002-39-03/S0273-0979-02-00941-2/S0273-0979-02-00941-2.pdf.
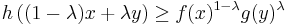
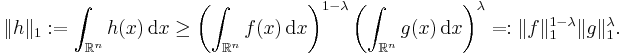
![\mathop{\mathrm{ess\,sup}}_{x \in \mathbb{R}^{n}} f(x) = \inf \left\{ t \in [- \infty, %2B \infty] | f(x) \leq t \mbox{ for almost all } x \in \mathbb{R}^{n} \right\}.](/2012-wikipedia_en_all_nopic_01_2012/I/217b61ca6917f76c0911ef61b74fe501.png)